Ejemplo
Una empresa de mensajería que opera en la ciudad tarda una media de 35 minutos en llevar un paquete, con una desviación típica de 8 minutos. Supongamos que durante el día de hoy han repartido 200 paquetes.
a) ¿Cuál es la probabilidad de que la media de los tiempos de entrega de hoy esté entre 30 y 35 minutos?.
Consideremos la variable X = “Tiempo de entrega del paquete”. Sabemos que su media es 35 minutos y su desviación típica, 8. Pero fijaos en que no sabemos si esta variable sigue una distribución normal. Durante el día de hoy se han entregado n = 200 paquetes. Es decir, tenemos una muestra x1, x2, ..., xn de nuestra variable.
Por el teorema del límite central sabemos que la media muestral se comporta como una normal de esperanza 35 y desviación típica:
8 √200 = 0,566
Si utilizamos esta aproximación, ya podemos contestar a la pregunta a. Debemos calcular:
Que es aproximadamente igual a la probabilidad siguiente:
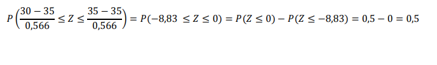
En otros casos se presente esta formula:
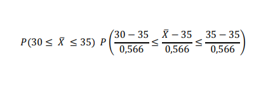
Escribe tu comentario